Plan and Elevation

https://study.com/

この2つの用語 Plan and Elevation が出てくる話はなんでしょうかと聞かれたら，まず「計画」と「標高／高度」が思い浮かぶので，登山か飛行の話かなと思ってしまいますが，これは日本の中1数学の教科書でいう投影図の中の平面図と立面図に当たります．

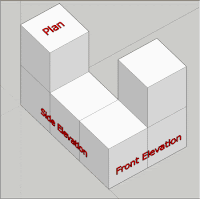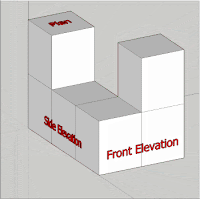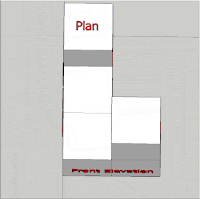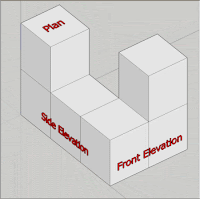
a) Plan
真上または真下から見た図．建築物のfloor plan といえば間取図という意味になります．

b) Elevation
立面図と側面図を合わせて縦面の図．見る方向によって front elevation, side elevation などと呼ばれ，建築物の外観を表すのによく使われています．

Graphical projection（投影図）は立体を平面上に描いた図の総称なので，他にもいろいろあります．

oblique projection (WikipediA)

Haese Mathematics 社の "MATHEMATICS FOR YEAR 8 (Fifth Edition)"では，次の2つが紹介されています．

c) oblique projection（斜投影図）の代表的なものでcabinet projection（キャビネット投影法）
＝正面は長さの比を変えず、奥行きだけ2分の1にして，座標軸を45°の傾きで描く．

d) isometric projection（等角投影図／等軸測投影図／等測投影法）

isometric projection (WikipediA)

＝すべて長さの比を変えず，座標軸を30°の傾きで描く．

以上4つは座標軸に平行に描くので，parallel projection（平行投影図）の一種になります．

さらに，座標軸にparallelにならないものがあります．

e) perspective projection（透視投影図）
この中には遠近法による 1 point perspective（一点透視），2 point perspective（二点透視），3 point perspective（三点透視）などがあります．Sketch（見取図）を実物と見た目をできるだけ同じように書くなら，3 point perspective が最も適しているといえます．

http://art-design-glossary.musabi.ac.jp

[Plan and Elevation 問題]

SPM Mathematics

The diagram shows a solid consisting of a right prism and a half-cylinder which are joined at the plane HICB. The base ABCDEF is on a horizontal plane. The rectangle LKJG is aninclined plane. The vertical plane JDEK is the uniform cross-section of the prism. AB = CD = 2cm. BC = 4cm. CM = 12cm.
Draw to full scale
(a) The plan of the solid
(b) The elevation of the solid on a vertical plane parallel to ABCD as viewed from X.
(c) The elevation of the solid on a vertical plane parallel to DE as viewed from Y.
(by SPM Mathematics)

解答はこちら

[Reference]

Net, Plan & Elevation of 3D Shapes
https://study.com/academy/lesson/net-plan-elevation-of-3d-shapes-lesson-for-kids.html

Graphical projection
https://en.wikipedia.org/wiki/Graphical_projection

Perspective Projection
http://art-design-glossary.musabi.ac.jp/perspective-projection/

Plan and Elevation, Long Question
http://spmmathematics.blog.onlinetuition.com.my/2015/11/plan-and-elevation-long-question_9.html

Lagrange's Notation, Leibniz's Notation

日本の高校数学の教科書では，Notation for Differentiation（微分の記法）について「関数$y=f(x)$の導関数を$f'(x)$で表し，$y'$や$\frac{dy}{dx}$などで表すこともある」と紹介されていますが，それぞれの記法を使い始めた人の名前まではあまり紹介されていません．

Lagrange's Notation (prime notation)$$y'=f'(x),\ y''=f''(x),\ y^{(4)}=f^{(4)}(x),\ y^{(n)}=f^{(n)}(x)$$$$f_x(x,y), \ f_{xx}(x,y), \ f_{xy}(x,y)$$日本では$y'$をワイダッシュ，$f'(x)$をエフダッシュエクスと読むことが多いですが，英語では"y prime"，"f prime of x"と読むのでprime notationともいいます．2行目は偏微分の記法で，こちらはsubscript（添え字）を使うのでsubscript notationのひとつになります．

Leibniz's Notation (differential notation)$$\frac{dy}{dx}=\frac{d}{dx}f(x), \quad \frac{d}{dx}\left( \frac{dy}{dx}\right)=\frac{d^2y}{dx^2}$$$$\frac{\partial f}{\partial x}, \ \frac{\partial^2 f}{\partial x^2}, \ \frac{\partial^2 f}{\partial x \partial y}$$$\frac{dy}{dx}$は"the derivative of y with respect to x"と読みますが，短く言う場合は，分数のように"dy over dx"とは読まず，単に"dy dx"と読みます．分数ではないのですが，置換積分のときに，$\frac{dx}{dt}=g'(t)$を形式的に$dx=g'(t)dt$として分数のように扱うことで式変形が容易になっています．

偏微分の$\frac{\partial f}{\partial x}$は，"the partial derivative of f with respect to x"とか"the partial derivative of f in the x direction"と読みますが，"dee f dee x"，"del f del x"，"day f day x"などと短く言うことがあります．$\partial$単独では"curly dee"，"rounded dee"などと言います

IB Mathematics Standard Level (Oxford University Press)

　
以上はよく使われる記法ですが，他にも次のような記法があります．

Euler's Notation (D notation or operator notation)$$Dy=Df, \ D^2y=D^2f$$$$\ D_xf, \ D_{xx}f, \ D_{xy}f$$この表記は多変数の関数でよく使われます．例えば$D_xf$は"D sub x of f"と読みます．

Newton's Notation (Dot Notation)$$\dot{y}, \ \ddot{y}$$この表記はkinematics（運動学）でよく使われ，時刻tにおける位置をyとするとき，velocity（速度）を$\dot{y}$，acceleration（加速度）を$\ddot{y}$で表します．

[Lagrange's Notation, Leibniz's Notation 問題]

Let x be the number of thousands of units of an item produced. The revenue for
selling x units is $r(x) = 4 \sqrt x$ and the cost of producing x units is $c(x) = 2x^2$
a) The profit $p(x)=r(x)-c(x)$. Write an expression for $p(x)$.
b) Find $\frac{dp}{dx}$ and $\frac{d^2p}{dx^2}$.
c) Hence find the number of units that should be produced in order to maximize
the profit.
(IB Mathematics Standard Level (Oxford University Press) exercise 7Y 5)

解答はこちら

[Reference]

IB Mathematics Standard Level (Oxford IB Diploma Programme 2012)
by Paul La Rondie,‎ Ed Kem,‎ Laurie Buchanan,‎ Jim Fensom,‎ Jill Stevens

Notation for differentiation
https://en.wikipedia.org/wiki/Notation_for_differentiation

The Notation of Differentiation
http://web.mit.edu/wwmath/calculus/differentiation/notation.html

∂
https://en.wikipedia.org/wiki/%E2%88%82

How do you pronounce (partial) derivatives?
https://math.stackexchange.com/questions/120504/how-do-you-pronounce-partial-derivatives

Wrapping Function

歌い方のひとつを意味する"rap"という単語と同じ発音ですが，wのついた方の"wrap"は「包む」という意味です．ではwrapping functionとは何を包む関数なのでしょうか．

Wrapping functionは，直線x=1上のすべての実数$t\in\mathbb{R}$が，
①Unit Square（単位正方形=原点(0, 0)を左下の頂点とする1辺の長さ1の正方形）
②Unit circle（単位円=原点(0, 0)を中心とする半径1の円）
を包みます．

① Wrapping Function of unit square

$W : \mathbb{R}\to\mathbb{R}^2 : t\mapsto (c, s) : W(t)=(c, s)$
ここで，W(t)=(c, s)は，点(1, 0)と(1, t)を結ぶ線分が(1, 0)を基点にして反時計回りにunit square（単位正方形）を包んだ先端の座標になります（t<0の場合は時計回り）．

例えば，t=3のときは，(1, 0)と(1, 3)を結ぶ線分が(1, 0)を基点にして反時計回りに単位正方形を包むと，先端は(0, 0)に達するのでW(3)=(0, 0)になります．他の具体例をいくつかあげましょう．

W(1)=(1, 1)

W(1.5)=(0.5, 1)

W(2)=(0, 1)

W(4.2)=(1, 0.2)

W(-4.2)=(0.8, 0)

この場合，0≦t＜4または-4＜t≦0で1周を包むことができ，4≦|t|なら重なって2重，3重…と包むことになります．

② Wrapping Function of unit circle

$W : \mathbb{R}\to\mathbb{R}^2 : t\mapsto (\cos{t}, \sin{t}) : W(t)=(\cos{t}, \sin{t})$
つまり，W(t)=(cost, sint)は，点(1, 0)と(1, t)を結ぶ線分が(1, 0)を基点にして反時計回りにunit circle（単位円）を包んだ先端の座標になります（t<0の場合は時計回り）．

例えば，t=3のときは，(1, 0)と(1, 3)を結ぶ線分が(1, 0)を基点にして反時計回りに単位円を包むと，先端は(cos3, sin3)に達するのでW(3)=(cos3, sin3)=(-0.98999, 0.14412)になります．他の具体例をいくつかあげましょう．

W$\left(\frac{π}{6}\right)=\left(\cos\left(\frac{π}{6}\right), \sin\left(\frac{π}{6}\right)\right)=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$

W$\left(\frac{π}{4}\right)=\left(\cos\left(\frac{π}{4}\right), \sin\left(\frac{π}{4}\right)\right)=\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$ 

W$\left(\frac{π}{2}\right)=(0, 1)$

W$(π)=(-1, 0)$

W$\left(-\frac{π}{2}\right)=(0, -1)$

この場合，0≦t＜2πまたは-2π＜t≦0で1周を包むことができ，2π≦|t|なら重なって2重，3重…と包むことになります．包んでいる様子がわかるものをGeogebraのサイトで見つけたので確認してみてください．

[Wrapping Function 問題]

Q1. Consider a special type of function called a wrapping function. This function, denoted by W, wraps a vertical number line whose origin is at R(1, 0) around a unit square, as shown at the right. With each real number t on the vertical number line, W associates a point P(x, y) on the square. For example, W(1)=(1,1) and W(-1) = (0,0). From W we can define two simpler functions:
      c(t)=x-coordinate of P,
and s(t)=y-coordinate of P.
a. Find W(2), W(3), W(4), and W(5).
b. Explain why W is a periodic function and give its fundamental period.
c. Explain how the periodicity of W guarantees the periodicity of c and s.
d. Sketch the graphs of u=c(t) and u=s(t) in separate tu-planes.

Q2. (Writing) Suppose the unit square in Q1 is replaced with the unit circle. Write a paragraph in which you describe how the wrapping function can
now be used to define the circular functions sine and cosine.

解答はこちら

[Reference]

Pearson Baccalaureate: Standard Level Mathematics for the IB Diploma
Ibrahim Wazir (Author),‎ Tim Garry (Author) : Pearson Education (22 Sept. 2008)

Essential Mathematics for Games and Interactive Applications, Third Edition
James M. Van Verth, Lars M. Bishop : A K Peters/CRC Press (2015/9/15)

The Wrapping Function
http://www.mhhe.com/math/precalc/barnettpc5/graphics/barnett05pcfg/ch05/others/bpc5_ch05-01.pdf

Transformations in two dimensions
http://orca.st.usm.edu/~jchen/courses/graphics/resources/book/chapter10transform2.pdf

The Sine and Cosine Function
http://bn002.weebly.com/uploads/5/8/3/3/58339589/trig_7.3.pdf