Slant Height

この用語は日本の教科書で使われているのを見たことがありませんが，英語の教科書ではよく使われています．日本語に直訳すると「斜高」すなわち「斜めの高さ」となりますが，いったいどういう意味なのでしょう．

Regular pyramid（正角錐 / 正多角錐）の slant height は，頂点から底面の一辺に下ろした垂線の長さを意味します．またright cone (直円錐) の slant height は，母線の長さを意味します．従って，slant height は正角錐と直円錐に共通の用語であり，下図の赤線部分の長さになります．普通の錐の高さは，altitude, height, perpendicular height, vertical heightなどという言い方があり，slant height はまったく違ったものになります．

ところで，面白いことに pyramid と cone で，right と regular に次のような意味の違いがあります．

        right pyramid（直角錐）        regular pyramid（正角錐）

        right cone（直円錐）             regular cone（普通の円錐形）

"right (直)" は，頂点から降ろした垂線が底面の重心を通るもので，底面が長方形や楕円のときもあり得ます．"regular (正)" は，角錐の場合，底面が正多角形かつ"right"なもの（例えば正四角錐）ですが，円錐の場合は「普通の」という意味になり，"regular cone"で検索するとアイスクリームの普通のコーンが多数現れます（笑）．

母線は generatrix, generating lineとも呼ばれます．Generate は生成するという意味なので直訳すると「生成線」となります．生成線は回転体を生む，母は子を生む，なので生成する線を母線と呼ぶことにしたのでしょう．そうすると，回転して円柱ができる回転軸に平行な線分も母線になります．また，回転して一葉双曲面ができる回転軸に対してねじれの位置にある線分も母線ということになります．従って，generatrix は線分の回転体たちに共通の用語ということになります．

因みに，神戸のポートタワーは，遠くから見ると一葉双曲面に見えますが，地面に対して垂直な軸に対して少しねじれの位置になる柱を多数使っていて，まるで向きの違う2本の柱が回転してできているように見えます．その様子をGeoGebraで作ってGIFにしてみました．

[Quiz]

京都タワー，大阪通天閣，神戸ポートタワーを高い順に並べると？

[Answer] (drag below)

①京都タワー(131m)　②神戸ポートタワー(108m)　③大阪通天閣(103m)

なお，電気工事用語で電気を分岐させるための「母線」は busbar（ブスバーまたはバスバー）というそうです．

[Reference]

Wikipedia : Pyramid (geometry)

https://en.wikipedia.org/wiki/Pyramid_(geometry)

電気工事用語集　母線

https://koujishi.com/glossary/busbar/

Exclusive Form

日本の中高数学の教科書では，frequency distribution table（度数分布表）を作成するときに，class（階級）の interval（区間）を　”at least / less than（以上/未満）" で表すのが普通ですが，英語のテキストを見ると，離散的な（連続でない）値はほぼ "at least / at most（以上/以下）" で表されています．例えば，100点満点の試験で60点台を表すのに，日本では「60以上70未満」で表すことが多いですが，英語のテキストでは「60以上69以下」という表し方が多く見られます．

そのため，アメリカの Microsoft社の表計算ソフト "Excel" の FREQUENCY（階級ごとに度数を返す）関数は、度数を「以上/以下」で数えますから，「以上/未満」でデータを数えたい場合は、FREQUENCY関数ではなくCOUNTIFS関数を使って度数を数えることになります．

英語ではこれらの表し方には名前がついていて，「以上/未満」の場合は "Exclusive Form (or Continuous Form)"，「以上/以下」の場合は "Inclusive Form (or Discontinuous Form)" と呼ばれています．直訳すると，「除外型」と「包含型」になりそうですが，日本語のテキストではこれらの用語が使われているのを見たことがありません．次の英文はその解説のひとつです．

There are two methods of classifying data according to the class intervals.
1) Exclusive Form (or Continuous Form):
When the class intervals are so formed that the upper limit of one class is the lower limit of the next class it is known as exclusive form. In this form, the upper limit of a class is not included in the class. Thus, in class 0-10, the value 10 is not included. It is counted in the next class 10-20.
2) Inclusive Form (or Discontinuous Form):
The classes are so formed that the upper limit of a class is included in that class. In class 1-10, the values lie between 1 and 10, including both 1 and 10. 

(CK-12.org)

いくつかの英語の本やサイトで，inclusive form をexclusive formに変換するのに，ひとつの階級の上限と次の階級の下限との差を2で割ったものを，全階級の下限から引き，全階級の上限に加えるという方法…①が紹介されています．例えば下図左の59と60との差 1 を2で割ると0.5なので，全階級の下限から0.5を引き，全階級の上限に0.5を加えます．すると下図右のような「以上/未満」型のexclusive formになります．

しかし，次のようにひとつの階級の上限と次の階級の下限との差を，全階級の上限に加える方法…②もあります．例えば下図左の59と60との差は 1 なので，全階級の上限に 1 を加えます．このほうが整数の「以上/未満」型 exclusive formに慣れている人には分かり易いかもしれません．

①は小数第 1 位で四捨五入して整数にしてから階級分けをすることと同じで，②は四捨五入せず小数のままで階級分けすることと同じです．例えば59.8は，①では上から2つ目，②では一番上の階級に入ることになります．

[Reference]

CK-12 : Classification of Data and Frequency Distribution - Definition, Methods, Steps and Examples
https://flexbooks.ck12.org/cbook/ck-12-cbse-maths-class-8/section/14.1/primary/lesson/classification-and-tabulation-of-data/

Class Interval
https://byjus.com/question-answer/convert-the-given-class-intervals-in-exclusive-form/

Office Hack : ExcelのFREQUENCY関数の使い方｜データの度数分布を垂直配列で返す
https://office-hack.com/excel/frequency/

Solid Angle

Plane angle（平面角）は，日本では高校の必履修「数学Ⅰ」の三角比まで 45° や 90° などの degrees（度数法）を使いますが，「数学Ⅱ」の三角関数からは微分積分で威力を発揮する radians（弧度法）を使います．弧度法は半径1の円の一部分（すなわち弧）の長さで表すので，一周なら 360°=2π，半周なら 180°=π，直角なら 90°=π/2 と表します（単位：radian）．

Solid angle（立体角）はその3次元への拡張なので，この訳が特に「意外」というわけではありませんが， 高校では扱われないので多くの人が「そんな角もあったのか」と思うことでしょう．

平面角は1点に集まる2辺の間の広がり具合を表すのに対し，立体角は1点に集まる面がつくる空間の広がり具合を表します．その定義はというと，平面角は半径1の円の扇形の中心角を弧の長さで表すのに対して，錐体の頂点に集まる面がつくる立体角は，その頂点を中心とする半径1の球面がその錐体と交わる部分の面積で表します．角錐なら spherical polygon（球面多角形），円錐なら spherical circle（球面円）（または spherical cap（球冠）ともいう）の面積になります．

例えば，右図のように，半径1の球の中心を頂点とする三角錐の，その頂点に集まる3平面がつくる立体角は，この球面上の黒い部分（球面三角形）の面積になります．平面上の三角形は3つの直線で囲まれた図形ですが，それと同じように球面三角形は3つの球面直線で囲まれた図形です．（注）球面幾何学において球面直線は大円（球と同じ半径の球面上の円）のことをいいます．なのでどの2本の球面直線も平行にはならず，必ず2点で交わります．

球面多角形や球面円は球面上の図形なので，平面上よりも膨らんでいる分だけその面積は大きくなります．また，それらを求める公式もよく知られています．

（球面の半径を1とします）

　①球面n角形　$S=\sum_{i=1}^n\theta_i-(n-2)\pi$　　($\theta_i$は内角，Harriot's theorem)

　　例えば球面三角形は$S=\theta_1+\theta_2+\theta_3-\pi$になります．

　②球面円　$\omega=2\pi\left(1-\cos\theta \right)=2\pi h$　　($\theta$は下図の角，$h$は球面円の高さ)

一般にこのような球面上の一部分の面積は次のように積分を使って求めることができます．

z軸となす角がθでx軸となす角がφである位置ベクトルを持つ球面上の点(sinθcosφ, sinθsinφ, cosθ)（上図の赤い点）を含む微小長方形dωは，経線方向の長さがdθ，緯線方向の長さがsinθdφなので，面積はそれらの積になります．$$d\omega=d\theta \cdot \sin\theta d\phi$$よって立体角ωはこの両辺を積分して，次の式で求められます．$$\omega = \displaystyle \int \int \sin\theta d\theta  d\phi $$

円錐の頂点の立体角は，先に述べたように球面円の面積になります．下図はsphere（球面）とspherical cone（球面円錐＝円錐と球面円のつながった立体）（またはspherical sector（球面扇形）ともいう）です．球の中心を頂点とし，z軸を中心軸とし，母線とz軸のなす角がθである球面円錐を考えると，底面である球面円は 0≦φ<2πとなるので，上の式から次のように立体角 ω（上の公式）が求まります．

$$\begin{eqnarray}\omega&=&\displaystyle \int_0^{2\pi} d\phi \displaystyle \int_0^\theta \sin\theta d\theta \\ &=& 2\pi \left[ -\cos\theta \right]_0^\theta \\ &=& 2\pi(1-\cos\theta)\end{eqnarray}$$例えばθ=π/6 (30°)のとき，立体角は次の値になります（単位：steradian）．$$\begin{eqnarray}\omega&=&2\pi\left(1-\cos\frac{\pi}{6} \right)\\ &=& 2\pi \left(1-\frac{\sqrt{3}}{2}\right)\\&=&(2-\sqrt{3})\pi\\&\approx&0.268\pi \end{eqnarray}$$これで球面円のない円錐の部分だけだったら，底面の面積は$\pi \sin^2\displaystyle\frac{\pi}{6}=\pi \left( \displaystyle\frac{1}{2} \right)^2=0.25\pi$なので，それより膨らんでいる分だけ大きくなっていますね．同じ計算で，θ=π/3 のときは ω=π，θ=π/2（半球）のときは ω=2π，特に θ=π（全球）のときは ω=4π になって球の表面積に一致します．

因みに，上の2θを円錐の apex angle（頂角）といいますから，円錐の頂角がπ/3のときの立体角は$0.268\pi$，円錐の頂角がπ（半球）のときの立体角は$2\pi$，円錐の頂角が2π（全球）のときの立体角は$4\pi$ということになります．

[Reference]

Solid angles in perspective

https://arxiv.org/ftp/arxiv/papers/2108/2108.05226.pdf

Acid Solution

数学で mixture problem（混合問題）と呼ばれるものに，次のようなものがあります．
　(1) 四則演算の混じった計算問題
　(2) 濃度の異なる溶液を混ぜる問題
　(3) 微分方程式の初期値境界値問題

数学用語ではなく化学用語の acid solution（酸溶液）は上の(2)の問題によく登場します．数学で solution といえば｢解｣という意味に使われますが，化学では｢溶液｣という意味があります．日本では濃度の異なる溶液を混ぜるのは salt water（食塩水）の問題が定番ですが，海外では acid solution がよく使われます．その種類はシュウ酸溶液，クエン酸溶液，グルコン酸溶液などいろいろありますが，酸の種類は特定されずに出題されることが多いです．例えば次の問題

An acid solution was made by mixing 5 gallons of an 80% acid solution and 7 gallons of a 50% acid solution. Find the concentration of acid in the new mixture.  (GreeneMath.com)

を 一次方程式で解くと次のようになります．

Let $x$ = the concentration of acid in the new mixture.

\begin{eqnarray}(5+7)\times\frac{x}{100}&=&5\times\frac{80}{100} + 7\times\frac{50}{100}\\ (5+7)x&=& 5\times80 + 7\times50\\ 12x&=&750\\x&=&62.5\end{eqnarray}

So, the concentration of acid in the new mixture is 62.5%.

解き方は食塩水の問題と同じなのですが，食塩の溶解度は100gの水に対し36g（水温20℃）なので，飽和濃度は 36÷136≒26(%) ですから，食塩水の濃度はそれ以下の設定にしなければいけません．それに対して acid solution の場合は濃度が 100% まであり得ますから，このようにどんなに高い濃度でも問題にすることができます．因みに 100%（純性）の acid は pure acid といいます．混合問題には，他にも alcohol（アルコール） や copper（銅）も使われます．それぞれ 100% のものはpure alcohol,  pure copper と呼ばれます．

余談ですが，砂糖の溶解度は 100g の水に対して 200g なので，これならどんな濃度でもOKかと一瞬思ってしまいますが，よく考えると，濃度は 200÷300≒67(%) が最大ですね．

[Question] (The answer follows after reference)

A local chemist made a solution that was 14% acid. He started out with 12 gallons of a 12% acid solution. He then added an unknown number of gallons of a 20% acid solution. How many gallons of the 20% acid solution did the chemist add to the initial acid solution?   (GreeneMath.com)

[Reference]

Mixture Word Problems Lesson
https://www.greenemath.com/College_Algebra/49/Mixture-ProblemsLesson.html

[Answer] (Drag below)

Let $x$ = the # of gallons of a 20% acid solution.

\begin{eqnarray}0.14(x+12)&=&0.2x+0.12\times12\\14(x+12)&=& 20x +144 \\ 14x+168&=&20x+144\\-6x&=&-24\\x&=&4\end{eqnarray}

So, the # of gallons of a 20% acid solution is 4.

Proof by Contradiction

｢$x^2$が偶数ならば$x$は偶数である」とか「兵庫県民は神戸市民である」など，正しい（真）か 正しいとは限らない（偽）かがはっきり判断できることを述べたものを proposition（命題）といい，それを証明するのに direct proof（直接証明）が難しい場合は indirect proof（間接証明）を使います．その代表的なものに，対偶による証明と背理法があります．

Hypothetical proposition（仮言命題）｢PならばQである」の contrapositive（対偶）｢QでないならPでない」を示すこと，すなわち対偶による証明は proof by contrapositive といいます．元の命題とその対偶の真偽が一致するのでこの方法が使えるわけですが，その理由は高校数学の教科書に必ず載っていますので見てみてください． 

一方，categorical proposition（定言命題）｢AはQである」の結論を否定すると矛盾が起こることを示す背理法は proof by contradiction といいます．この contradiction は矛盾という意味なので，背理法は直訳すると ｢矛盾による証明｣ ということになります．背理とは ｢道理に背く」ことなので，矛盾と同じような意味になりますが，よくある日本語の証明の中では「道理に背く」とはいわずに「矛盾する」という言い方をするので，これは「矛盾による証明」と訳した方が良かったのではないかと思います．

同様に訳し方がおかしいと思うものに，rational number（有理数），irrational number（無理数）があります．rational は合理的，irrational は非合理的という意味なので，「じゃあ無理数は非合理的なんかい!」と文句をいいたくなります．もともと ratio が比という意味なので，整数の比で表せる「有比数」または「可比数」と，そうでない「無比数」または「不可比数」にした方が良かったと思います．

さて， 背理法といえば，①｢$\sqrt{2}$は無理数である」ことの証明が有名で，どの高校数学の教科書にも載っています．他にも ②｢素数は無限に存在する」や ③｢円の接線は接点を通る半径に垂直である」という命題が有名です．

②は日本の中高の教科書には登場しません．Euclid's Elements（ユークリッドの原論）Book Ⅸ の Proposition 20 に少しわかりにくい証明が載っていますが，もっと分かり易い証明がネット上で簡単に見つかりますので探してみてください．

③は事実のみが中1の教科書から登場するのに，中高教科書のどこにもその証明がありません．あまりにも当たり前なことのように見えるからだと思われます．この証明もユークリッドの原論にありますので，詳しく見てみましょう．

Proposition 18 (Book Ⅲ) 

"If a straight line touches a circle, and a straight line is joined from the center to the point of contact, the straight line so joined will be perpendicular to the tangent."

Euclid's Elements

続いて証明があります．分かり易く意訳してみます．

円ABCの中心をFとし，点Cにおける接線を直線DEとします． 

DE⊥FCでないと仮定，すなわち結論を否定します．

すると，Cとは別にDE⊥FGとなる点Gが接線DE上にあるはずです．

その点Gが存在するなら，∠FGCの方が直角になり，∠FCGは鋭角になります．すると直角三角形FGCの斜辺はFCとなり，これは他の辺より長いはずなので

FG<FC

となるはずです（この図ではそのように見えませんが，DE⊥FGと仮定すればこうなります）．

しかし，実際はFG>FB=FC， すなわち

FG>FC

なので矛盾します.

DE⊥FCでないと仮定したことで矛盾が起こりました．

ゆえにDE⊥FCが成り立つ，すなわち円の接線は接点を通る半径に垂直であるということが，背理法によって証明されました．

[Question] (The answer follows after reference)

Prove there are no integers a and b such that 10a + 15b = 1.

(by StudySmarter)

[Reference]

Euclid's Elements   Book III   Proposition 18
http://aleph0.clarku.edu/~djoyce/elements/bookIII/propIII18.html

StudySmarter "Proof by Contradiction"
https://www.studysmarter.us/explanations/math/pure-maths/proof-by-contradiction/

[Answer] (Drag bellow) 

Let us assume that we could find integers a and b that satisfy such an equation. We can then divide both sides by 5 to give 2a + 3b = 1/5. If a and b are integers, and we multiply each by another integer (2 and 3 respectively, in this case), then sum them, there is no possible way that this could result in being a fraction, which is what the above condition requires. This leads us to a contradiction. Thus, there are no integers a and b such that 10a + 15b = 1.

Inverse

Inverse は主に｢逆｣という意味で，次のような場合に使われています．

・inverse operation（逆演算）：例えば $+$ に対して $-$, $\times$ に対して $\div$．

・inverse function（逆関数）：例えば $y=2x$ に対して $y=\frac{1}{2}x$，$y=e^x$ に対して $y=\log_{e}x$．

・inverse element（逆元）：例えば opposite（反数）は $a$ に対する $-a$ で additive inverse（加法逆元）といい，また reciprocal（逆数）は $a$ に対する $\frac{1}{a}$ または$a^{−1}$で multiplicative inverse（乗法逆元）といいます．

ここまでは意外でもなんでもないのですが，日本の高等学校必履修｢数学Ⅰ｣ の proposition（命題）に関する用語｢逆，裏，対偶｣を意味する英語は次のようにになっています．

・ conditional statement（条件文）：P implies Q（PならばQ）P$ \implies $Q

に対して，次の3つが定義されています．

・converse statement（逆） : Q implies P（QならばP）Q$\implies$P

・inverse statement（裏） : ~P implies ~Q（PでないならQではない）~P$\implies$~Q

・contrapositive statement（対偶） : ~Q implies ~P（QでないならPではない）~Q$\implies$~P

ここでは，仮定と結論を入れ替えたものが converse（逆），仮定と結論をそのまま否定したものが inverse（裏）となっていて，inverse が｢逆｣ではないので少し混乱してしまいますね．英和辞典（英ナビ！辞書）を調べてみると，converse には｢逆，反対｣の意味がありますが，inverse には｢逆，反対｣に加えて｢裏表，裏腹｣という意味もありました．誤訳や間違いというわけではなさそうです．

[Question] (The answer follows after reference)

What is the inverse statement of the following conditional statement?
"If $x=1$, then $x^2=1$."

(a) If $x\neq1$, then $x^2=1$.
(b) If $x\neq1$, then $x^2\neq1$.
(c) If $x^2=1$, then $x=1$.
(d) If $x^2\neq1$, then $x\neq1$.

 

[Reference]

Converse, Inverse, and Contrapositive of a Conditional Statement
https://www.chilimath.com/lessons/introduction-to-number-theory/converse-inverse-and-contrapositive-of-conditional-statement/

Converse, Inverse, and Contrapositive
https://www.mometrix.com/academy/converse-inverse-and-contrapositive/

[Answer] (Drag bellow) 
An inverse statement assumes the opposite of each of the original statements. The opposite of “If x=1” would be “If x≠1.” The opposite of “then x²=1” would be “then x²≠1.”  Then answer is (b).

LCD

visualpharm.com

LCDといえば，テレビやパソコンでお馴染みの Liquid Crystal Display（液晶ディスプレイ）を思い浮かべます．また似ている用語では，照明に使われるLEDですが，これは Light Emitting Diode（発光ダイオード）の略になります．｢いまさら聞けない｣豆知識という感じですね．

数学関連で似ているものは，LCM = Least Common Multiple（最小公倍数），GCD = Greatest Common Deviser（最大公約数），GDC = Graphing Display Calculator（グラフ電卓）などがあります．ややこしいですね．

注）最大公約数は，他にもGCM (Greatest Common Measure) またはGCF (Greatest Common Factor) または HCF (Highest Common Factor) と言う場合があります．

さて，LCDは数学用語ではどういう意味なのでしょうか．これは，Least Common Denominator または Lowest Common Denominator といって，日本語では｢最小公分母｣といい，複数の分数の分母の最小公倍数を意味します．例えば，2と3の最小公倍数は6なので，｢$\frac{1}{2}$と$\frac{1}{3}$のLCDは6である｣という言い方をします．日本ではこの用語はほとんど聞いたことがないのですが，英語の解説にはよく登場します．

因みに，｢通分する｣ことを英語では次のようにいいます．

        reduce (the fractions) to a common denominator

例えばこんな言い方があります．

        Add 1/2 to 1/3 by reducing the fractions to a common denominator
        LCD(1/2, 1/3)=LCM(2, 3)=2×3=6 so that 1/2+1/3=3/6+2/6=5/6

"reduce" はもともと｢減らす｣という意味なので，｢通分がなぜ reduce?｣と思ってしまいますが，通分は｢複数の分数を共通の分母でひとつにまとめる｣すなわち｢複数の分数を共通の分母でひとつに減らす｣という意味もあるので，この用語が使われているのだと思われます．

ところで，通分には次のような言い方もあります．どの表現を使われても意味が分かるようにしておきたいですね．

        put ~ over a common denominator
        change ~ to equivalent fractions with a common denominator

実は｢約分する｣というのも"reduce"を使います．こちらは約分すれば分母・分子の値が減少するので，この用語で違和感はありません．通分にも約分にも同じ"reduce"を使うことになるわけですが，後に続く文が少し違います．

        reduce (a fraction) to its lowest terms（既約分数まで約分する）

この用語のおかげで，reducible（可約），irreducible（既約）といった言い方も覚えやすくなります．ただ，約分にも simplify, cancel という別の言い方もあるので，やはりどの表現を使われても意味が分かるようにしておきたいですね．

覚えておきたい関連した用語は他に次のものがあります．

        like fraction（分母の等しい分数）　(c.f.) like term（同類項）
        bottom number / denominator（分母）
        top number / numerator（分子）

[Question] (The answer follows after reference)

What is the LCD for the following three fractions?
1/18, 1/24 and 1/30

[Reference]

Least Common Denominator - LCD
https://www.cuemath.com/numbers/least-common-denominator-lcd/

[Answer] (Drag below)

360

Sextic

Sex は「性」や「性別」などの意味があるので，sexual, sexy は「性的な」という意味になります．それなら sextic も同様の意味ではないかと思ってしまいますが，これは全く異なる意味の数学用語で， 形容詞なら「6次の」，名詞なら「6次式」という意味になります．6 なら six だろうと思いますが，数学用語は Latin（ラテン語）や Greek（ギリシャ語）が語源になっているものが多く，これも Latin で 6 を表す sex を語源としています．なので，例えば sextic function なら6次関数という意味になります．

両言語の数詞をまとめてみました．

数学用語以外にも，monotone, duet, triathlon など，これらが頭につくものがたくさんありますね．

[Quiz] 1960年代に「ドリフターズ」から分裂して活躍した4人組コミックバンド（のちに5人になった）のグループ名は「○○○○カルテット」．○○○○は何？

[Answer] （次の行をドラッグしてください）

Donkey Quartet（ドンキーカルテット）

紀元前，1年が10か月だった時代，今の August（8月）は Sextilis（6番目の月）と呼ばれていました．その後 January, February が加わって12か月になっても名称は変わりませんでしたが，後にローマ皇帝 Augustus が自分の名を使って August に変えました．因みに，7月も Quintilis（5番目の月）だったのを，あの Julius Caesar が 同じく自分の名をとって July に変えました．しかし，September から December は当初の意味から2か月ずれたまま残っています．

意外なところでは，16進法を hexadecimal または sexadecimal と言うのに対し，60進法は sexagecimal と言いますが，hexagecimal とは言わないようです．

次数の表現です．

1変数の sextic equation（6次方程式）は一般に次式で表されます．$$a_6x^6+a_5 x^5+a_4x^4+a_3x^3+a_2x^2+a_1x+a_0=0$$Abel–Ruffini theorem（アーベル–ルフィニの定理）により，5次以上の方程式は代数的に（四則演算と累乗根で）解けないのですが，Galois theory（ガロア理論）から，ある条件を満たすときは代数的に解けることが分かっています．例えば次のような特別な形なら$x^3$を変数とする2次方程式として代数的に解くことができます．$$a_6x^6+a_3x^3+a_0=0$$必ず解ける代数的でない（超越的な）解法はあるのですが，あまりにも複雑なので，実用的には数値計算で解を求めるのが一般的です．

Cayley's sextic

次の2変数 sextic equation（6次方程式）を Cayley's sextic といいます．これは他の人が最初に発見したのですが，Cayley が詳しく研究したのでこの名前がついています．$$64 (x^2+y^2)^3-48 ax (x^2+y^2)^2-3 a^2(x^2+y^2)(5 x^2+9 y^2) -a^3 x^3=0$$

a=-1のとき　　                                   a=1のとき

これはよく知られた Cardioid（心臓形）上の任意の点における接線に原点から降ろした垂線の足の軌跡（pedal curve＝垂足線）になっています．

内側の曲線がCardioid (Wolfram MathWorld)

[Reference]

Sextic equation

https://en.wikipedia.org/wiki/Sextic_equation

Cayley's Sextic

https://mathworld.wolfram.com/CayleysSextic.html

Cardioid Pedal Curve

https://mathworld.wolfram.com/CardioidPedalCurve.html

Nature of Roots

この nature を「自然」と訳すと，nature of roots は「根っこの自然」となって，これは植物学的な話かなと思ってしまいます．数学ではどんな場面に登場しているのか見てみましょう．

Use the discriminant to determine the nature of the roots of quadratic equation. 

これなら「2次方程式の根（こん）の自然を決めるには判別式を使う」となりますが， nature には次の意味もあります．

Weblio英和対訳辞書 "nature"
自然、天然、自然界、自然力、自然現象、(人・動物の)本性、天性、性質、本質、特質

なので「2次方程式の根（こん）の性質を調べるには判別式を使う」ということになります．しかし discriminant（判別式）で判別するのは，2次方程式の解が「two distinct real roots（異なる2つの実数解），multiple roots（重解），imaginary roots（虚数解）」（複素数を未習の場合は「虚数解」ではなく「解なし」）のどれになるかということですから，「性質」というのも少し違う気がします．

続いて "nature of" の意味を調べてみると，

Weblio英和対訳辞書 "nature of"
[単数形で; 通例修飾語を伴って] 種類, [the nature] 〔ものの〕本質，特質，特徴 

というわけで，nature of roots は「根（解）の種類」と訳すのが正しいようです．したがって，上の文章は「2次方程式の根（解）の種類を決めるには判別式を使う」という意味になります．日本の高校数学Ⅱの教科書でも，「解の種類を判別する」という言い方が使われています．

ところでもともと判別式は，n次方程式が重解を持つ条件を与える式として，19世紀中ごろに英国の数学者 Sylvester が導入しました．$n$次方程式 $$a_nx^n+a_{n-1}x^{n-1}+\cdot\cdot\cdot+a_1x+a_0=0 \quad (a_n \neq 0)$$ の重複を含めた解を $\alpha_1, \cdot\cdot\cdot, \alpha_n$ とすると，$$\prod_{i<j}(\alpha_i-\alpha_j)=0$$になるとき，すなわちすべての異なる（はずの）解の差の積が0になるとき，どれか2つ以上の解が一致するので重解を持ちます．Sylvester はさらに虚数の平方は負になることから虚数解を判別するためにこの式を平方し，式の値を分数にしないようにするために$a_n^{2n-2}$を掛けて，判別式$D$を次の式で与えました．$$D=a_n^{2n-2}\prod_{i<j}(\alpha_i-\alpha_j)^2$$例えば$n=3$なら，$D=a_3^{2･3-2}(\alpha_1-\alpha_2)^2(\alpha_2-\alpha_3)^2(\alpha_1-\alpha_3)^2$となり，これが3次方程式の判別式になりますが，これだけでも計算はかなり複雑です．

では$n=2$にしてみましょう．$$D=a_2^{2･2-2}(\alpha_1-\alpha_2)^2$$ここで2次方程式を $ax^2+bx+c=0$，その重複を含めた解を$\alpha$，$\beta$とすると，解と係数の関係より，$\alpha+\beta=-\frac{b}{a},\quad\alpha\beta=\frac{c}{a}$なので，\begin{eqnarray} D &=& a^2(\alpha-\beta)^2 \\&=&  a^2(\alpha^2-2\alpha\beta+\beta^2) \\&=& a^2\left( (\alpha+\beta)^2-4\alpha\beta \right)  \\ &=& a^2\left( \left(-\frac{b}{a}\right)^2-4\left( \frac{c}{a}\right)  \right)  \\&=& b^2-4ac \end{eqnarray}というわけで，お馴染みの2次方程式の判別式を導くことができました．

[Question] (The answer follows after reference)

Find the value of the discriminant, and state the nature of the roots for each equation. (Mathematics SL : Oxford University Press)

a) $x^2+5x-3=0$
b) $2x^2+4x+1=0$
c) $4x^2-x+5=0$
d) $x^2+8x+16=0$

[Reference]

Weblio英和対訳辞書

Discriminant
https://en.wikipedia.org/wiki/Discriminant

代数方程式の判別式
http://hooktail.sub.jp/algebra/Discriminant/

[Answer] (Drag below)

a)     37 ; two  different real roots
b)     8 ; two different real roots
c)     -79 ; no real roots
d)     0 ; two equal real roots

Vertex Form

Polygon（多角形）や polyhedron（多面体）などの図形では，2本以上の辺が集まっている点のことを vertex（頂点）といいます．多面体の頂点 (V)，辺 (E=edge)，面 (F=face) の数に関する Euler's polyhedron theorem （オイラーの多面体定理）$V-E+F=2$ は有名ですよね．

Quadratic function（二次関数）のグラフの形は parabola（放物線）といいますが，その向きが変わる点のことを頂点といい，英語では vertex または turning point といいます．そしてその頂点の座標$(p,q)$がすぐにわかるように表した式$$y=a(x-p)^2+q\tag{1}$$を vertex form といいます．直訳すると頂点形ということになりそうですが，日本語ではこう呼ばれず，基本形と呼ばれています．ところが，これを英語に直訳して basic form というと， $y=ax^2$ を意味することになります．なので式(1)は，英語では vertex form，日本語でも基本形ではなく頂点形と呼ぶ方がよさそうです．

一方，次のように展開された式(2)は general form（一般形）と呼ばれています．$$y=ax^2+bx+c\tag{2}$$この式(2)を式(1)に変形することを，completing square（平方完成）といいます．

さらにもうひとつ，次の式(3)で2次関数を表す方法があります．$$y=a(x-\alpha )(x- \beta)\tag{3}$$これは factorize（因数分解）された形なので factored form（因数分解形 or 分解形），または$x$ intercept（$x$切片）$\alpha$，$\beta$がすぐに分かる形なので intercept form（切片形）とも呼ばれています．

上の式(1)と(2)は Standard Form（標準形）と呼ばれることもあり，話が少しややこしくなります．

■式(1)を Standard Form（標準形）と呼んでいる例
(英) https://mathsgee.com/9601/what-is-the-standard-form-of-a-quadratic-function
(日) http://wakarimath.net/explanation/q.php?pID=E00008
■式(2)を Standard Form（標準形）と呼んでいる例
(英) https://www.turito.com/learn/math/quadratic-functions-in-standard-form
(日) https://kaz-academy.com/math-koshiki22/

基本，標準，一般という用語の定義が曖昧であることが原因です．このような〇〇形といういい方は，日本の教科書では使われていないのですが，実際，日英の多くの参考書やサイトでは当たり前のように使われています．

ついでに，他にも 〇〇form といういい方があるので日英で調べてみました．

■Linear Function（一次関数）/ Equation of a Line（直線の方程式）
slope-intercept form　$y=mx+k$　基本形ともいう
standard form（標準形）　$ax+by=c$
general form（一般形）        $ax+by+c=0$
intercept form（切片形）　$\displaystyle \frac{x}{a}+\frac{y}{b}=1$
point-slope form  $y-y_1=m(x-x_1)$
two-point form  $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1) $
vector form  $\vec{p}=\vec{a}+t\vec{d}$  or  $\boldsymbol{p}=\boldsymbol{a}+t\boldsymbol{d}$

■Equation of a Circle （円の方程式）
center-radius form　$(x-p)^2+(y-q)^2 = r^2$　標準形または基本形ともいう
general form（一般形）　$x^2 + y^2 +lx + my + n = 0$

以上のことから，グラフの特性である頂点や傾き切片や中心半径などがすぐに分かる式の形はその名前を使って頂点形，傾き切片形，中心半径形などと呼び，それを展開した形は一般形と呼ぶのが良いのではないでしょうか．何でも英語に合わせるが良いというのではなく，なるべく意味の曖昧な言葉を使わない方が良いと思います．

Aliquot

｢約数｣という日本語は，他にも「因数」や「因子」などの言い方がありますが，英語でも divisor, measure, factor, submultiple, aliquot などいろいろな言い方があります．最初の3つは，GCD (Greatest Common Divisor), GCM (Greatest Common Measure), HCF (Highest Common Factor) と表すと，いずれも「最大公約数」を意味します．あまり使われませんが，greatest common submultiple という場合もあります．しかし，aliquot だけは少し違った意味があります．

数学英和･和英辞典（共立出版）には，

aliquot　a. 割り切れる，整除できる． n. 割り切れる数，約数． ～ part 約数．

と書かれているので，これだけでは aliquot も同じ｢約数｣という意味ではないかと思いますが，実は多くの場合，aliquot または aliquot part というのは proper divisor（真約数），すなわちそれ自身を含まない約数を意味します．例えば12の divisors は 1, 2, 3, 4, 6, 12ですが，12の aliquot は 1, 2, 3, 4, 6になります．

関連するものに aliquot sum（アリコット和）, aliquot sequence（アリコット数列）があります．aliquotだけ和訳がないのは不思議ですが，元々Latin語の ali (otherの意) とquot (how manyの意)から来ているそうです．

aliquot sequence（アリコット数列）

正の整数$k$の全約数の総和を$\sigma(k)$と表します．aliquot sum すなわち proper divisor の総和は，全約数の総和からそれ自身を引くので，$\sigma(k)-k$となります．$k$に対して，aliquot sum を返す関数$s(k)=\sigma(k)-k$を "restricted divisor function"といいます．正式な日本語訳はありませんが，強いていうなら意訳して「真約数関数」でしょうか．

aliquot sequence は，正の整数$k$から始まり，次の項がその前の項の restricted divisor function の値，すなわち aliquot sum になるという，次の漸化式を満たす数列です．$$s_0=k,\quad \quad s_{n+1}=s(s_n)=\sigma(s_n)-s_n$$例1. $k=4$のとき，\begin{eqnarray}s_0&=&4\\s_1&=&s(s_0)=\sigma(s_0)-s_0=\sigma(4)-4=(1+2+4)-4=1+2=3\\ s_2&=&s(s_1)=\sigma(s_1)-s_1=\sigma(3)-3=(1+3)-3=1\\ s_3&=&s(s_2)=\sigma(s_2)-s_2=\sigma(3)-3=1-1=0\end{eqnarray}

例2. $k=6$のとき，\begin{eqnarray}s_0&=&6\\s_1&=&(1+2+3+6)-6=1+2+3=6\\ s_2&=&(1+2+3+6)-6=1+2+3=6\end{eqnarray}

例3. $k=220$のとき，

\begin{eqnarray}s_0&=&220\\s_1&=&1+2+4+5+10+11+20+22+44+55+110=284\\ s_2&=&1+2+4+71+142=220\end{eqnarray}

例1は最後が「素数→1→0」となって終ります．例2は aliquot sum がそれ自身に一致する complete number（完全数）なので，同じ数が繰り返されます．例3はお互いが相手の aliquot sum になる a pair of amicable numbers（友愛数）なので，2数が交互に現れます．他にも3つ以上の数を繰り返す sociable numbers（社交数）があります．以上で aliquot sequence のパターンがすべて尽くされているとする Catalan-Dickson conjecture（カタラン-ディクソン予想）は，2022年4月現在，未解決問題となっています．

[Reference]

Aliquot sequences
https://www.unirioja.es/cu/jvarona/aliquot.html

aliquot part
https://www.daviddarling.info/encyclopedia/A/aliquot_part.html

Bin

缶は英語でも can といいますが，瓶は bin ではなく bottle といいます．bin には蓋つきの容器やごみ箱という意味があるので「物を入れる」という点では瓶と似ています．さらにこの bin には数学用語でも2つの意味があります．

■binary（2進法）

decimal（10進法）は，ある数を0から9までの整数10個を係数に使って10の冪（べき）の和で表したとき，その係数を並べて表します．例えば234は，$$\begin{align} 200+30+4&=2\times10^２+3\times10^1+4\times10^0\\&=234\end{align}$$一方， binary（2進法）は，ある数を0と1のみを係数に使って2の冪の和で表したとき，その係数を並べて表します．例えば10進法の 234 は，$$\begin{align} 234&= 128+64+32+8+2\\ &= 2^7+2^6+2^5+2^3+2^1\\&=1\times2^7+1\times2^6+1\times2^5+0\times2^4+1\times2^30\times2^2+1\times2^1+0\times2^0\\&= 11101010_{(2)}\end{align}$$となり，2進法では$11101010_{(2)}$と表されます．

因みに，ファイルの拡張子で".bin"というのがありますが，テキストファイル".txt"以外のファイル，すなわち binary file のことで，2進数で表現されています．

■frequency distribution table（度数分布表）の class（階級）

frequency distribution table の class のことを bin ともいい，ある区間ごとに分類された小グループのひとつひとつ（histogram の各棒）を意味します．data binning とは、全データをいくつかの bin に分けることをいい，data bucketing ともいいます．data を分けて容器またはバケツに入れるというイメージでしょう．したがって，histogram を作ることも data binning のひとつといえます． 

# of data（データの数）を $n$ とし，それらを $x_1, x_2, ...., x_n$とします．すると，# of bins（階級の数）$k$ と bin width（階級の幅）$h$ との関係は次式で与えることができます．$$k=\frac{\max x_i-\min x_i}{h}\tag{1}$$または$$h=\frac{\max x_i-\min x_i}{k}\tag{2}$$つまり，$k$と$h$はデータの範囲を比例定数とする反比例の関係になります（値が整数にならない場合は切り上げます）．

例えば，ある100点満点の試験を27名が受験した結果が次の値だったとしましょう．

76, 57, 47, 100, 47, 55, 83, 57, 49, 68, 73, 55, 68, 87, 91, 89, 37, 72, 63, 62, 57, 30, 77, 25, 60, 12, 66

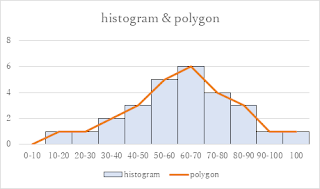
$k$=10を上の式(2)に当てはめると，$$h=\frac{100-0}{10}=10$$すると$k$=10のとき$h$=10になり，frequency distribution table と graph は上図のようになります．しかし，特にこの値にしなければならないわけではありません．$$\frac{100-0}{5}=20$$なので，$k$=5のとき$h$=20，$k$=20のとき$h$=5になります．また，$$\left\lceil\frac{100-0}{7}\right\rceil=\left\lceil14.2857....\right\rceil=15$$

$\left\lceil\quad\right\rceil$は切り上げをする関数 ceiling function（天井関数）

なので，$k$=7のとき$h$=15，$k$=15のとき$h$=7になります．

この# of bins $k$とbin width $h$は data をよく眺めて直接決めてもいいのですが，実はこれらの適切な値についてはこれまでかなり研究されており，"choice"，"rule"，"formula"などと呼ばれる方法が知られています．# of data（データの数）$n$を基準にしたもの，SD=standard deviation（標準偏差）$\sigma$，IQR=interquartile range（四分位範囲）を使うものなどいろいろありますが，その中で$n$を基準にして$k$を求めるものは次の3つがあります．

① Square-root choice$$\displaystyle k=\lceil {\sqrt {n}}\rceil\displaystyle $$② Rice Rule（1944年）$$\displaystyle k=\lceil 2\sqrt[3]{n}\rceil \displaystyle$$

③ Sturges' formula（1926年）$$\displaystyle k=\lceil \log _{2}n\rceil +1$$$n$=27を代入すると，いずれも$k$=6になりますから，# of data $n$=27のときは # of bins $k$=6が適切ということになります．

①②③のグラフ

また，# of data $n$とSD=$\sigma$を使って$h$を求めるものに次式があります．

④ Scott’s Rule（1979年）$$\displaystyle h = \left\lceil\frac{3.49\sigma}{\sqrt[{3}]{n}}\right\rceil$$上の例の$\sigma$=20.7なので，$$\displaystyle h=\left\lceil\frac{3.49\times 20.7}{\sqrt[3]{27}}\right\rceil=\left\lceil24.08....\right\rceil=25$$となり，bin width $h$=25，# of bins $k$=4が適切ということになります．

[余談]

●Excel で frequency distribution table を作るときに frequency を求める，すなわち多数のデータの中から各 bin width（階級の幅）の度数を数える方法は，「データ分析」「FREQUENCY関数」などを使うより「COUNTIFS関数」を使う方が比較的容易にできました．例えば，ある条件範囲から0以上10以下の数を数えるには次のように入力します．

=COUNTIFS (条件範囲, ">=0", 条件範囲, "<10")

●Excel で histogram と frequency distribution polygon（度数分布多角形）を重ねて描く方法をいろいろ試してみたところ，「挿入→ヒストグラム」「データ分析→ヒストグラム」から描くよりも次の方法が比較的容易でした．
1) グラフを描く準備として，上図のような3列（一番左の列はセルの書式設定で文字列にしておく）を作る.
2) その3列を選択
3) 挿入→おすすめグラフ→すべてのグラフ→組み合わせ→集合縦棒と折れ線→OK（棒グラフと折れ線グラフができる）
4) グラフの縦棒の上で右クリック→データ系列の書式設定→要素の間隔→0%（棒グラフがヒストグラムに変わる）→色を変える

●Excel で frequency distribution table を作る前の生データから histogram だけを作るときは「挿入→ヒストグラム」が楽です．Binの幅が自動的に決まって描かれますが，横軸部分を右クリックし、メニューから「軸の書式設定」を選択して，ビンの幅，ビンのオーバーフロウ，ビンのアンダーフロウを適切に決めればOKです．

[Reference]

Histogram

https://en.wikipedia.org/wiki/Histogram

Histogram – The Ultimate Guide of Binning

https://www.answerminer.com/blog/binning-guide-ideal-histogram

Cartesian plane

MathsLinks

ここでの plane は飛行機ではなくて平面という意味です．2D（2次元）のグラフを描くのに xy-plane（xy平面）を使いますね．これは coordinate（座標）を使うので coordinate plane（座標平面）ともいいます．

日本では以上の2つの言い方が多いのですが，英書では1637年に著書「方法序説」で座標を考案した René Descartes（1596-1650）の名をとって Cartesian plane（デカルト平面）と呼ばれることが多いです。

なぜデカルトなのに，Cartesian（英語発音「カーティージャン」）と呼ぶのかというと，ラテン語名が Renatus Cartesius（レナトゥス・カルテシウス）というからなんです．日本語ではデカルトがよく使われているので，初めて Cartesian と聞くと誰のことだか分かりませんね．

2D以上の場合も含めると，Cartesian coordinate system（デカルト座標系）といい，orthogonal coordinate system（直交座標系）あるいはrectangular coordinate system（長方形座標系または矩形座標系）といういい方もあります．

[Quiz]
デカルトの著書『方法序説』（Discours de la méthode）の中の有名な言葉で，"I think, therefore I am." の日本語訳は何でしょう？

[Answer]（この下の行をドラッグしてください）
我思う、ゆえに我あり

因みに，Cartesian product（デカルト積）または direct product（直積）という集合があります．これは，複数の集合から1つずつ要素をとりだしてできる組の集まりのことで，例えばA= {1, 2, 3}とB= {a, b}の Cartesian product A×Bは{(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)}になります．

2Dの Cartesian plane の座標は，(2, 3)とか$(\sqrt{2},\pi)$とかの（実数，実数）の形で表されるので，実数の集合$\mathbb{R}$と$\mathbb{R}$の Cartesian product $\mathbb{R}×\mathbb{R}$の要素になります．

また，$y=2x+3$，$x^2+y^2=4$， $z=x^2+y^2$ などの，2Dならxとy，3Dならx, y, zを用いる関数の表し方を Cartesian equation（デカルト方程式） といいます．それに対するものとして，polar equation（極方程式）やvector equation（ベクトル方程式）などがあります．例えば，原点中心で半径3の円を表す polar equation $r=3$，vector equation $|\vec{p}|=3$ は，$\sqrt{x^2+y^2}=3$ より，Cartesian equation は $x^2+y^2=9$となります．

[Cartesian plane 問題]
Eliminate the parameter t to find a simplified Cartesian equation of the form.
(1)  $x=2-t$，$y=6-3t$

(2)  $x=\cosh t$，$y=\sinh t$

正解はこちら

[Reference]

MathsLinks

https://mathslinks.net/links/cartesian-plane

Hemisphere

Math Hemisphere Emoji Clip Art

半円のことを semicircle といいますね．Circle は円ですから，semi は半分という意味になります．他にも quadrant（4分の1円），three quarter circle（4分の3円）といういい方があります． 

Quadrantは「象限」の訳語だとばかり思っていたので，「4分の1円」という意味があるのは意外だったのですが，もっと意外だったのはもともと「四分儀」という天体の高度を観測するのに用いられた機器のことであって，quadrant が「象限」を意味するのは2次元平面上だけだということです．つまり，x軸とy軸で分かれる quad（4つの）領域だけが  quadrant と呼ばれるわけです．

また，3次元における「象限」は，x軸とy軸とz軸で分かれる oct（8個の）領域なので octant といい，これももともとの意味は「八分儀」（天体の高度や水平方向の角度を測るための道具）です．

なので，次元に関係なく「象限」は，quadrant でも octant でもなく，一般に orthant というのが正しいようです．従って，n次元空間には $2^n$個の orthant（象限）が存在するということになります．

さて， 半円のことを semicircle というので，半球は semisphere なのかと思ったら，hemisphere といいます．もともと semi はラテン語起源，hemi はギリシア語起源だそうですが，なぜこのような違いになったのか不思議ですね．

[Quiz]
北半球はNorthern hemisphere．では南半球は？

[Answer]（この下の行をドラッグしてください）
Southern hemisphere

頭にsemiがつくものは他に，semiannual（年に2回），semifinal（準決勝）などがあります．また，hemiがつくものは，hemicylinder（円柱を縦に半分に切った雨どいのような形）があります．

因みに，demiもフランス語で半分の意味があり，tasseがコーヒーカップという意味なので，demitasse coffeeは小さいカップに入れたコーヒーのことをいいます．

そしてさらに，イギリス英語で quaver は音楽用語の8分音符，semiquaver は16分音符，demisemiquaver は32分音符，hemidemisemiquaver は64分音符という意味なんです．これは驚きですよね．

[Hemisphere 問題]
Calculate the spherical layer's volume that remains from the hemisphere after the v(=3) cm section is cut. The height of the hemisphere is r(=10) cm.     (Hemisphere Problems)

正解はこちら

[Reference]

円や楕円、半円、三日月形って英語で何て言うの？
https://dreamcometrue358.com/around_circle/

象限
https://ja.wikipedia.org/wiki/%E8%B1%A1%E9%99%90

Semi-, hemi-, and demi-
https://grammarist.com/prefix/semi-hemi-and-demi/

Hemisphere Problems
https://www.hackmath.net/en/word-math-problems/hemisphere

Vinculum

「分数の分子と分母の間の線」にも名前があります．日本では日頃あまり意識しないし，使うこともないのですが，実は2通りの呼び方があります．

① vinculum（括線）
② fraction bar（分数線）

ところが，これらは他にもいろいろな意味があるので話が少々ややこしくなります．

まず以下の横線部分はすべて vinculum と呼ばれています．

1. radical（根号）$\sqrt{12345}$ 
2. repeating decimals（循環小数）$0.\overline{123}$
3. line segment（線分）$\overline{AB}$
4. complex conjugate（共役複素数）$\overline{z_1+z_2}$
5. negation of a logical expression（論理式の否定）$\overline{A∧B}$

さらに，$3-(2+1 )=3-\overline{2+1}$のように，括弧の代わりに使うこともできるようですが，この使い方はほとんど見ることがなく，ネットで探したらインドのものばかりでした．

つまり，vinculum は「分数の分子と分母の間の線」というよりは，その線の下の数式や文字式を括って（くくって）いる線（括線）のことだということになります．

[Quiz]
$\frac{3}{4}$は英語で何と読むでしょう？正しいものをすべて選びなさい．
①three quarters　②three over four　③three divided by four　④three by four　⑤quotient of three and four　⑥ratio of three to four　⑦three fourths

[Answer]（この下の行をドラッグしてください）

すべて正解．（ただし，three by four は 3×4 を意味する場合もあります．divided by， multiplied by を by だけに省略した形です．読み方ですから式を見て判断できます）

Fraction Bars

じゃあ vinculum ではなく，fraction bar の方が直訳で分かり易いのかなと思ったら，これも主には右図のような長方形を分割して分数を表したもののことをいいます．小学生の分数計算の学習によく使われているものですが，これにはさらに別名があって，fraction strips（日本語では「分数タイル」）とも呼ばれています．

ということは，vinculum も fraction bar も「分数の分子と分母の間の線」という意味を持つが，よく使われる別の意味もあるということです．ややこしいですね．

因みに，日本語で括線（かっせん）と同じ読みの数学用語である割線は，円や曲線のグラフ上の2点を通る直線のことで secant といいますが，この secant も reciprocal circular functions（割三角関数）の secant（正割）$\sec x=\frac{1}{\cos x}$という別の意味もあります．

さらに数学用語でない「かっせん」は他にもあり，cock（活栓）は管などを開閉するもの，live line（活線）は電流の通じている電線，battle（合戦）は雪合戦などのような「戦い」を意味します．

[vinculum 問題]
Express $0.\overline{1}+0.\overline{12}+0.\overline{123}$ as a fraction and decimal.
正解はこちら

[Reference]

What’s the line in a fraction called?
https://caterpickles.com/2017/11/28/whats-the-line-in-a-fraction-called/

Vinculum
https://mathworld.wolfram.com/Vinculum.html

Math.net Fraction bar
https://www.math.net/fraction-bar

Shear Transformation

いつもは英文の中で見つけた数学用語で意外なものを紹介することが多いのですが，この用語はその逆で，「等積変形」の英訳は何かを調べてみた結果の紹介です．

「等積変形」は日本の中学数学2の教科書に登場します．広い意味では，図形の面積を一定にしたまま形を変えることですが，ここでは特に三角形や平行四辺形で底辺の長さと高さを同じにしたまま，頂点や上辺を底辺に対して平行移動させることを意味しています．

[Quiz]

右図の三角形の面積は？

[Answer]（この下の行をドラッグしてください）
2×5÷2＝5

用語や短文などの翻訳や説明を互いに助け合うサイト KudoZネットワーク で，「等積変形」という用語に関して，その回答がnative speakerや英語教育従事者などからいくつか寄せられていました．それだけ適切な訳語が見つからない用語のひとつということになります．

find another shape with the same area

isometric transformations

equal area transformation

equivalent deformation

shaving the shape

shear transformation

congruence transformation

これらのうちほぼ「等積変形」と訳して良さそうなものは始めの4つですが，実際，英語のサイトでこの用語を使って，ここでいう「等積変形」を説明しているのを見つけることができません．また，equivalent は「命題の同値（⇔）」，congruent は「図形/整数の合同（≡/≅）」の意味で使われるのが定番ですから，これらをさらに「等積」の英訳とするのは難しい気がします．

Shear（せん断）は，もともと「刈る」とか「ハサミで切る」という意味ですが，平面幾何では上の方法で図形を変形させるという意味があり，これは"Translation"で紹介した shear transformation（直訳は「せん断変換」）と同じ意味になっています．実際，この用語だけは，検索するとその意味の内容のものが見つかります．したがって，shear transformation こそ，少し意訳になりますが「等積変形」を英訳する用語として最も適切ではないでしょうか．

[Shear Transformation 問題]
図のように4点A=(1, 5)，B=(-1, 3)，C=(2, 1)，D=(1, 0)と，底辺が$x$軸上にあって上辺が点Aを通る四角形EFGHがある，この折れ線で分けられている左右の部分の面積が変わらないように，点Aを通る直線で左右を分けるとき，この直線の方程式を求めよ．
正解はこちら

[Reference]

等積変形
https://jpn.proz.com/kudoz/japanese-to-english/mathematics-statistics/1154281-%E7%AD%89%E7%A9%8D%E5%A4%89%E5%BD%A2.html

Closure Property

いきなりクイズです．

[Quiz]

日本の数学Ⅲの教科書に登場する平均値の定理は次の誰の名前がつくでしょう？

①ロル　②ラグランジュ　③コーシー　④テーラー

[Answer]（この下の行をドラッグしてください）

②ラグランジュ

日本の教科書では数学用語として名前の出てこない概念や定理・公式などが，実は英語ではちゃんと名前があるという場合があります．

■発見者の名前がついていない例

Lagrange's mean value theorem（ラグランジュの平均値の定理）
平均値の定理はいくつかあります．その中で日本の高校数学Ⅲで登場する，「グラフ上の2点を結ぶ割線と等しい傾きを持つ接線がその間に存在する」という定理が「ラグランジュの平均値の定理」です．

Varignon's theorem（バリニョンの定理）
日本の中学数学2で出てくる「任意の四角形の各辺の中点を結んでできる四角形は平行四辺形になる」という定理です．

■用語として使われていない例

Scientific Notation（科学表記）
例えば$1.23×10^4$のような数の表し方（2021年度からの学習指導要領で中1で学ぶ内容から中3で学ぶ内容に移りました）をいいますが，日本の教科書では「（整数部分が1けたの数）×（10の累乗）の形」という言い方をしています．

Closure property も用語として使われていない例になります．日本語で「閉性」というので直訳で伝わりますが，日本の教科書では中学数学1と高校数学Ⅰで2回も登場するのに，この用語が使われていないというのが意外なのです．

例えば，整数×整数の結果は必ず整数になるので，このことを"the set of integers is closed under multiplication（整数の集合は掛け算について閉じている）"といいます．逆に，整数÷整数の結果は整数になるとは限らないので，"the set of integers is not closed under division（整数の集合は割り算について閉じていない）"といいます．

このような性質をclosure property（閉性）というのですが，日本の教科書にはこの用語は出てこず，「数の範囲と四則計算の可能性」といって，closedのことを「この範囲でいつでも計算できる」「その範囲で常に計算できる」というような言い方をしています．operation of arity two（2数の演算）の結果がまたその2数の属する集合の元になるという意味なので，この表現は少し違和感を感じますね．

このように2数（ある集合の元2つ）から1つの数（ある集合の元1つ）が得られる演算を，代数学ではbinary operation（二項演算）といい，一般には2つの集合A, Bの Cartesian product（デカルト積）A×B＝｛(a, b)｜a∈A，b∈B｝からその演算結果の集合C｛c｜c∈C｝へのmapping（写像）で定義されます．例えば$2\div 3=\frac{2}{3}$という計算は，(2, 3)を$\frac{2}{3}$に対応させており，この場合は，整数の集合と整数の集合のデカルト積$\mathbb{Z} \times \mathbb{Z}$から有理数の集合$\mathbb{Q}$へのmappingになっています．

「ある集合が，ある演算について閉じている」という場合は，A=B=Cのときをいい，例えば上の整数の集合$\mathbb{Z} $では，足し算，引き算，掛け算の結果がまた整数になるので，これら3つの演算については閉じているといえます．文献によっては，このように閉じている場合だけをbinary operationという場合があります．

代数学は，以上の事柄を基本として，単位元，逆元の存在，ひとつの演算についての交換法則，結合法則，2つの演算についての分配法則を用いて，群，環，体という概念を定義し，3次，4次，5次方程式解法の理論へと発展していきます．

[Closure Property 問題]
Is the set {-1, 1} closed under addition, subtraction, multiplication and/or division?
解答はこちら

[Reference]
Binary operation
https://en.wikipedia.org/wiki/Binary_operation
因みに，このサイトを参考にするのはいいのですが，日本語Wikiの「二項演算」というページは「この記事は検証可能な参考文献や出典が全く示されていないか不十分です」となっており，内容も英語版とかなり違っていてあまり参考になりませんでした（この投稿公開日現在）．

Elementary mathematics

どの国でもあると思いますが，その国で常識だと思われていることが，世界に目を向けたときに常識ではない，実はおかしいと感じることがよくあります．日本の教育関連で思いつくことをいくつか挙げてみると，
・年度始めが4月である．
・小学生だけがランドセルを使う．
・三学期だけ期間が短い．
・国立なのに女子大がある．
・教科名を小学校では「算数」，中学校以上では「数学」という．
etc....

[Quiz]
「数学」は英語で mathematics，または省略して math といいますが，小学校の教科名「算数」は英語でなんというでしょう？

[Answer]（この下の行をドラッグしてください）
 和英辞典にはarithmeticとあります．

逆にこの単語を英和辞典で調べると，算数の他に，算術，計算などの意味がありますが，算数以外の意味の方が近いように思われます．

しかも，この単語は英語圏で「算数」という意味にはとられないようです．日本の「算数」にあたる用語は，ずばり mathematics です．小学校で学ぶ math だと強調するなら elementary mathematics となります．ただこれは「初等数学」（大雑把に言えば小中高の数学）という意味にも使われているので，もう少し正確にいうと．elementary school mathematics となります．

海外の現地校やインターナショナルスクールの小中高は，六三三制よりも五三四制が多いので，日本の「算数」をもっと正確に言うなら，mathematics at Japanese elementary school になるでしょう．

「数について学ぶ」ことなので，小学校でも中学以上でも数学（math）ですよね．中国・台湾や韓国・北朝鮮でも小学校での教科名は「数学」だそうです．小学校だけ「算数」という名称を使っているのは日本だけのようです．日本の小学校でも「数学」で良いのではないでしょうか．

よく算数と数学の違いはこうだという，いかにももっともらしい説明をする書籍やサイト等が見られますが，後付けの印象を強く感じます．

平成29（2017）年改訂の小学校学習指導要領解説では，従来の「算数的」という表現を「数学的」に変え，「数学的活動を通して，数学的に考える資質・能力を育成することを目指す」とし，中高と同じような表現になりました．ところが教科名については，

小学校の時に具体物を伴って素朴に学んできた内容を，中学校では数の範囲を広げ，抽象的・論理的に整理して学習し直すことになる。そして，さらに高等学校・大学ではそれらが，数学の体系の中に位置付けられていく。以上のことから，小学校では教科名を「算数」とし，中学校以上の「数学」と教科名を分けている。

と書かれています．しかし，小学校では「具体的」で中学から「抽象的」になるからというのは，教科名を分ける理由にはなりません．具体的な数学もあれば抽象的な数学もあるからです．

文科省の他の文書も「算数・数学」とひとまとめにして述べる場合が多く見られますが，これらをまとめて「数学」だけにすれば，文章もすっきりして読みやすくなるでしょう．

文科省は，世界標準の小中高カリキュラム "International Baccalaureate (IB)" を実施する日本の学校を増やすため，高校の最後の2年間のカリキュラムDiploma Program (DP)の6教科のうち4教科を日本語でできる「日本語ディプロマ」を普及させようとしています．このように教育のグローバル化を目指す中で，小学校だけ「算数」という呼び方を残すのは時代遅れのような気がします．

日本の小学校も教科名を「数学」にするべきだと思います．

[Reference]

英語で「算数」はなんと言うの？│ arithmeticじゃないよ
https://www.sanctio.net/arithmetic/

Duck’s Egg

Duckはカモやアヒルのことです．ドナルドダックというキャラクターがありますが，その絵から判断すると，ダックはアヒルだとばかり思っていました．ただ，アヒルではなくてカモであることを強調したいときはwild duckといいます．また，よく騙される人のことをカモといいますが，これはeasy markというそうです．

Eggは卵ですから，duck's eggはアヒルの卵という意味になります．ニワトリより少し大きいそうですが，味はどうなんでしょうか？ 一度食べてみたいものです．

さて，duck's eggの直訳はアヒルの卵となりますが，数学ではどんな意味があるのでしょう．これはその形から来ています．卵に似た数字は何でしょう？ そう，0ですね．なので数字の0を表すのかと思ったら，zero point，すなわち全く得点できない0点のことなんです．ずばり，スポーツや試験の点数が0点のときにduck’s eggといいます．別にduckのではなくても単にeggでいいと思いますけどね．

[Quiz]
ドラえもん（1969年～）の野比のび太よりずっと前からテストで0点を取ることで有名だった漫画のキャラクターは誰でしょう？

[Answer]（この下の行をドラッグしてください）
丸出ダメ夫（1964年 - 1967年 週刊少年マガジン）

Zeroが数字の0という意味なのは当然ですが，もうひとつ，zero of a function（関数の零点）という概念があります．関数$y=f(x)$があるとき，$f(x)=0$となる$x$をzeroといいます．例えば，$f(x)=(x-1)(x-2)$のzeroは，$x=1, x=2$になります．つまり，関数＝0という方程式の解のことです．英語ではzeroですが，日本語では零点といいます．

証明できたら100万ドル授与されるミレニアム問題のひとつであるリーマン予想は，ゼータ関数の自明でないzero（零点）の実数部分はすべて$\frac{1}{2}$であるというもので，2021年4月現在，未解決です．

因みに，oval（卵形線）と聞けば卵の形に近い曲線を思い浮かべますが，定義としては「内側の任意の2点を結ぶ線分がその曲線の中にある閉じた曲線」というもので，円や楕円はもちろん，陸上競技のトラックや三角形・四角形などの凸多角形も含まれます． 

Ellipse（楕円）の定義は，2つの焦点$S$, $T$からの距離の和$PS+PT$が一定である点$P$の軌跡で，2点からその距離より長い糸をピーンと張って描くことができます．

実際の卵の形に近い曲線としては，Ellipseに定義が似ている以下の2つが知られています．

■Cartesian oval（デカルトの卵形線）
2つの焦点$S(0,0)$, $T(c,0)$からの距離を$PS$, $PT$とするとき，$PS+mPT$が一定の値$d$である点$P$の軌跡で，方程式は次式になります．$$\left \{(1-m^2) (x^2+y^2)+2 m^{2}c x+d^{2}-m^{2} c^2 \right \}^2=4 d^{2} (x^2+y^2)\tag{1}$$これは2つの図形が現れ，定数の値によって，円や楕円や双曲線になったりします．GEOGEBRAで描いてみたので，定数をいろいろ変えてみてください．

なお，m=1の時は式$(1)$より楕円$$\left \{2c x+d^{2}- c^2 \right \}^2=4 d^{2} (x^2+y^2)$$となり，長軸を$2a$，短軸を$2b$として高校の教科書風に整理すると次式になります．$$\frac{\left(x-\frac{c}{2}\right)^2}{a^2}+\frac{y^2}{b^2}=1$$

Cartesian ovalは，アナログではEllipseと似た方法で描けますが，一方の糸だけ2重にするという方法をJames Clerk Maxwell (1831 - 1879)が見つけました．

＜描き方＞

            Ellipse      　　  　　　　           Cartesian Oval

■Cassini oval（カッシーニの卵形線）
2つの焦点$S(-c,0)$, $T(c,0)$からの距離の積$PS \times PT$が一定の値$d^2$である点$P$の軌跡で，方程式は次式になります．$$ (x^{2}+y^{2})^{2}-2c^{2}(x^{2}-y^{2})+c^{4}=d^{4}\tag{2}$$

Cassini Oval (c=5, d=4.9 のとき)

[Duck’s Egg 問題]

Prove (1) and (2).

正解はこちら

[Reference]
MacTutor Cartesian Oval
https://mathshistory.st-andrews.ac.uk/Curves/Cartesian/
MacTutor Oval Curves
https://mathshistory.st-andrews.ac.uk/Projects/Johnson/chapter-4/

Vanishing

この単語が邦題になっている映画が3つもあります．

●The Vanishing / Keepers（バニシング）2018年イギリス

無人島に灯台守としてやって来た3人の男の前に，金塊を大量に持った男とそれを追う男2人が現れ，金塊の争奪戦が起こります．

●The Vanishing（ザ・バニシング -消失-）1988年ドイツ

夫婦でオランダからフランスへ旅行に来たが，妻が突然いなくなり，夫が捜索するが見つからず，3年後に犯人から連絡が来ます．

●Live Like a Cop, Die Like a Man（バニシング）1976年イタリア

容疑者を次々に撃ち殺すので上司も手を焼いているという若い2人の刑事が，麻薬シンジケートの大ボスを追いかけます．

[Quiz]
新車を陸送する仕事の途中，スピード違反で警察に追いかけられても、ただひたすら車を走らせて逃げ続ける男を描いた1971年のアメリカ映画は何でしょう？

[Answer]（この下の行をドラッグしてください）
Vanishing Point

いずれも誰か，または何かがvanish（消失）する映画です．

さて前置きが長くなりましたが，数学で「消え失せる」なんていう意味の用語はあるのでしょうか．実は，値が0になることを vanish といいます．例えば関数$f(x)=(x-1)^2$は，$x=1$で$f(x)$の値が$0$ ($f(1)=0$) になりますから，このことを

the function $f(x)=(x-1)^2$ vanishes at $x=1$

と表します．単純に「$x=1$のとき$f(x)=0$」でいいんじゃないの？と思いますが，これも「少し気取った言い回し」（『数学版これを英語で言えますか？』保江邦夫著：講談社ブルーバックス）のひとつらしいので，こんな言い方も知っておいた方がよさそうです．

また，$x$が実数の時，関数$f(x)=\frac{1}{x^2+1}$は，$x$が大きくなるにつれて$f(x)$の値が0に近づきますが，このことを次のように言います．

the function $f(x)=\frac{1}{x^2+1}$ vanishes at infinity

さらに，vanish identically という場合がありますが，これはある時の値が$0$になるのではなく、恒等的に$0$に等しいということを意味しています．例えば，

$\sin ^2 \theta +\cos ^2 \theta -1$ vanishes identically

ということになります．

逆にどこも$0$にならない場合は、nonvanishingといい，例えば次のように表すことができます．

the values of $x^2+1$ are nonvanishing for real $x$

もちろん$x^2+1$は$x$が虚数の時にvanishすることがありますから，real $x$（実数の$x$）でないといけませんね．

因みに，3次式の因数分解をするには，factor theorem（因数定理）で因数をひとつ見つけた後，次の名前のついた2つの方法のいずれかですることができます．

① vanishing method$$\begin{align} x^3-19x-30 &= x^3+2x^2-2x^2-4x-15x-30\\ &= x^2(x+2)-2x(x+2)-15(x+2) \\&= (x+2)(x^2-2x-15)\\&= (x+2)(x^2+3x-5x-15)\\&= (x+2)\{x(x+3)-5(x+3)\}\\&= (x+2)(x+3)(x-5)\end{align}$$

② division method$$\begin{align} x^3-19x-30 &=  (x+2)(x^2-2x-15)\\&= (x+2)(x+3)(x-5))\end{align}$$①は無理やり因数を作っていく感じがしますが，「因数」→「値が0になる」→「消失する」ということでこんな名前がついたのでしょう．②は日本の高校の教科書に載っているやり方で，はじめに見つけた因数で割り算をする方法です．

[Reference]

Vanishing
https://mathworld.wolfram.com/Vanishing.html

Pizza Theorem

食べ物の名前のついた定理がいくつかあります．

Pancake Theorem（パンケーキの定理）は，「2つのパンケーキ（形は円でなくてもよいし，重なっていても離れていてもよい）は1つの直線でそれぞれを2等分できる」という定理で，それを3次元に拡張したものをHam Sandwich Theorem（ハムサンドイッチの定理）といいます．

Chicken McNugget Theorem（チキン・マックナゲットの定理）は，「互いに素な$m$個入り，$n$個入りパックの組み合わせで買えない最大の個数は$mn-m-n$個である」という定理で，もともとチキン・マックナゲットが9個入り，20個入りで販売されていたのが発祥の定理です．

Pizza Theorem（ピザ の定理）1968年
ピザ（この形は円でなければいけません）を，円内の任意の点Pを通る$2n$本の直線で中心角が$\frac{\pi}{2n}$ (radian) になる扇形みたいな図形$4n$個に分割したとき， 分割された各部分を2人で同じ方向に交互に取っていくと，その和がそれぞれ同じ面積になる．ただし，$n≥2$．

[Quiz]
n=1のときの分割は何本の直線でいくつに分割し，できたおうぎ形みたいな図形の中心角は何度でしょう？

[Answer]（この下の行をドラッグしてください）
2本の直線で4分割，中心角はπ/2(radian)＝90°

n=2のとき4本で8分割，n=3のとき6本で12分割

上図でいうと，n=2のときは紫色と黄色の部分，n=3のときは緑色と橙色の部分の面積が等しいという定理です（1999年には「$n$人で交互に取っていっても，その和がそれぞれ同じ面積になる」ことが示されました）．

n=1のとき，すなわち2本で4分割したときはなぜダメなのでしょう．

右図の円の半径をR，中心をOとします．点Pで直交する2本で4分割されたとして，中心Oを通る2本の直径とでできる9個の領域をa～iとすると，

　　右上+左下＝a+e+h+i+c＝a+(i+g)+(i+f)+i+c

                      ＞a+g+f+i+c＝$\frac{\pi R^2}{2}$

となり，右上+左下＞半分＞左上+右下になるからです．つまり，4分割では交互に取っても2人の取り分は同じ面積になりません．

n=2のとき，すなわち4本で8分割したときに定理が成り立つことを確認してみましょう．

右図で$PA=r(\theta)$，$PE=r(\theta+\frac{\pi}{4})$とすると，扇形みたいな形APEは，$\theta$を細かくすると，ほとんど扇形になるので，扇形の面積の公式$S=\frac{1}{2} r^2  \theta$より，$\varDelta S=\frac{1}{2} r(\theta)^2 \varDelta \theta$となりますから，この部分の面積$S_1$は$$S_1=\displaystyle \int_0^\frac{\pi}{4} \frac{1}{2}r(\theta)^2 d\theta$$となります．これから交互に4つ取ると，$$S_1+S_3+S_5+S_7=\displaystyle \int_0^\frac{\pi}{4} \frac{1}{2} \left \{ r(\theta)^2+r \left(\theta+\frac{\pi}{2}\right)^2+r(\theta+\pi)^2+r \left(\theta+\frac{3\pi}{2}\right)^2 \right \}d\theta$$となりますが，これは$$\displaystyle \int_0^\frac{\pi}{4} 2R^2d\theta\tag{1}$$となることが分かっていて（理由はこの後すぐ），するとこの続きは$$\displaystyle \int_0^\frac{\pi}{4} 2R^2d\theta=2R^2\displaystyle \int_0^\frac{\pi}{4} d\theta=2R^2 \left[ \theta \right] _0^\frac{\pi}{4}=2R^2\cdot\frac{\pi}{4}=\frac{\pi R^2}{2} $$となって，交互に取った1人分の面積はちょうど円の半分になることが分かります．

さて$(1)$の理由です．

$r(\theta)=PA=a$，$r(\theta+\frac{\pi}{2})=PB=b$，$r(\theta+\pi)=PC=c$，$r(\theta+\frac{3\pi}{2})=PD=d$とすると，$$R^2=OA^2=ON^2+NA^2=MP^2+NA^2=\left( \frac{b-d}{2}\right)^2+\left(\frac{a+c}{2}\right)^2$$$$R^2=OB^2=OM^2+MB^2=NP^2+MB^2=\left( \frac{a-c}{2}\right)^2+\left(\frac{b+d}{2}\right)^2$$辺々加えると，$$2R^2= \frac{1}{2}\left(a^2+b^2+c^2+d^2\right)$$となり，$(1)$が示されました．

因みに，Wolfram MathWorld には the second pizza theorem というのが紹介されていて，こう書かれてありました（笑）．

This one gives the volume of a pizza of thickness a and radius z:

pi z z a. 

 [Reference]

57. THE PIZZA THEOREM
https://web.maths.unsw.edu.au/~mikeh/webpapers/paper57.pdf

Pizza Theorem
https://mathworld.wolfram.com/PizzaTheorem.html